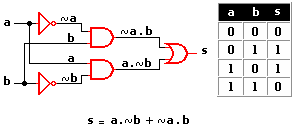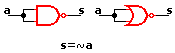circuito

Componente electrónico

Componentes electrónicos.

Se denomina componente electrónico a aquel dispositivo que forma parte de un circuito electrónico. Se suele encapsular, generalmente en un material cerámico, metálico o plástico, y terminar en dos o más terminales o patillas metálicas. Se diseñan para ser conectados entre ellos, normalmente mediante soldadura, a un circuito impreso, para formar el mencionado circuito.

Hay que diferenciar entre componentes y elementos. Los componentes son dispositivos físicos, mientras que los elementos son modelos o abstracciones idealizadas que constituyen la base para el estudio teórico de los mencionados componentes. Así, los componentes aparecen en un listado de dispositivos que forman un circuito, mientras que los elementos aparecen en los desarrollos matemáticos de la teoría de circuitos.

De acuerdo con el criterio que se elija podemos obtener distintas clasificaciones. Seguidamente se detallan las comúnmente más aceptadas.

1. Según su estructura física

• Discretos: son aquellos que están encapsulados uno a uno, como es el caso de los resistores, condensadores, diodos, transistores, etc.
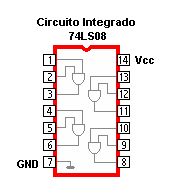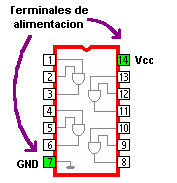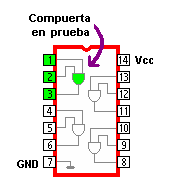
• Integrados: forman conjuntos más complejos, como por ejemplo un amplificador operacional o una puerta lógica, que pueden contener desde unos pocos componentes discretos hasta millones de ellos. Son los denominados circuitos integrados.

2. Según el material base de fabricación.

• Semiconductores
• No semiconductores.

3. Según su funcionamiento.

• Activos: proporcionan excitación eléctrica, ganancia o control
• Pasivos: son los encargados de la conexión entre los diferentes componentes activos, asegurando la transmisión de las señales eléctricas o modificando su nivel 

4. Según el tipo energía.

• Electromagnéticos: aquellos que aprovechan las propiedades electromagnéticas de los materiales (fundamentalmente transformadores e inductores).
• Electroacústicos: transforman la energía acústica en eléctrica y viceversa (micrófonos, altavoces, bocinas, auriculares, etc.).
• Optoelectrónicos:transforman la energía luminosa en eléctrica y viceversa (diodos LED, células fotoeléctricas, etc.).

Componentes semiconductores

Artículo principal: Componente semiconductor

También denominados como componentes de estado sólido, son los componentes "estrella" en casi todos los circuitos electrónicos. Se obtienen a partir de materiales semiconductores, especialmente del silicio aunque para determinadas aplicaciones aún se usa germanio. tambien sirven para que no pase altas cargas de voltaje

Componentes activos

Los componentes activos son aquellos que son capaces de excitar los circuitos o de realizar ganancias o control del mismo. Fundamentalmente son los generadores eléctricos y ciertos componentes semiconductores. Estos últimos, en general, tienen un comportamiento no lineal, esto es, la relación entre la tensión aplicada y la corriente demandada no es lineal.

Los componentes activos semiconductores derivan del diodo de Fleming y del triodo de Lee de Forest. En una primera generación aparecieron las válvulas que permitieron el desarrollo de aparatos electrónicos como la radio o la televisión. Posteriormente, en una segunda generación, aparecerían los semiconductores que más tarde darían paso a los circuitos integrados (tercera generación) cuya máxima expresión se encuentra en los circuitos programables (microprocesador y microcontrolador) que pueden ser considerados como componentes, aunque en realidad sean circuitos que llevan integrados millones de componentes.

En la actualidad existe un número elevado de componentes activos, siendo usual, que un sistema electrónico se diseñe a partir de uno o varios componentes activos cuyas características lo condicionará. Esto no sucede con los componentes pasivos. En la siguiente tabla se muestran los principales componentes activos junto a su función más común dentro de un circuito.

Componente	Función más común
Amplificador operacional	Amplificación, regulación, conversión de señal, conmutación.
Biestable	Control de sistemas secuenciales.
PLD	Control de sistemas digitales.
Diac	Control de potencia.
Diodo	Rectificación de señales, regulación, multiplicador de tensión.
Diodo Zener	Regulación de tensiones.
FPGA	Control de sistemas digitales.
Memoria	Almacenamiento digital de datos.
Microprocesador	Control de sistemas digitales.
Microcontrolador	Control de sistemas digitales.
Pila	Generación de energía eléctrica.
Tiristor	Control de potencia.
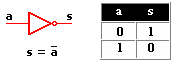
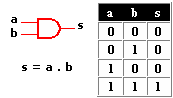
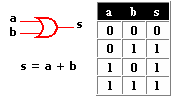
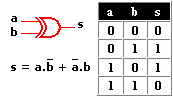
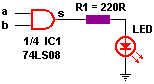
Puerta lógica	Control de sistemas combinacionales.
Transistor	Amplificación, conmutación.
Triac	Control de potencia.

Componentes pasivos

Son aquellos que no necesitan una fuente de energía para su correcto funcionamiento. No tienen la capacidad de controlar la corriente en un circuito.

Los componentes pasivos se dividen en :

Componentes Pasivos Lineales:

Componente	Función más común
Condensador	Almacenamiento de energía, filtrado, adaptación impedancia.
Inductor o Bobina	Almacenar o atenuar el cambio de energía debido a su poder de autoinducción.
Resistor o Resistencia	División de intensidad o tensión, limitación de intensidad.

Componentes Electromecánicos:

Interruptores, Fusibles y Conectores.

Componentes optoelectrónicos

Artículo principal: Componente optoelectrónico

Componentes optoeletrónicos, son aquellos que transforman la energía luminosa en energía eléctrica, denominados fotosensibles, o la energía eléctrica en luminosa, denominados electroluminiscentes.

sistemas numericos

Sistema Binario

El sistema de numeración más simple que usa la notación posicional es el sistema de numeración binario. Este sistema, como su nombre lo indica, usa solamente dos dígitos (0,1).

Por su simplicidad y por poseer únicamente dos dígitos diferentes, el sistema de numeración binario se usa en computación para el manejo de datos e información. Normalmente al dígito cero se le asocia con cero voltios, apagado, desenergizado, inhibido (de la computadora) y el dígito 1 se asocia con +5, +12 volts, encendido, energizado (de la computadora) con el cual se forma la lógica positiva. Si la asociación es inversa, o sea el número cero se asocia con +5 volts o encendido y al número 1 se asocia con cero volts o apagado, entonces se genera la lógica negativa.

A la representación de un dígito binario se le llama bit (de la contracción binary digit) y al conjunto de 8 bits se le llama byte, así por ejemplo: 110 contiene 3 bits, 1001 contiene 4 y 1 contiene 1 bit. Como el sistema binario usa la notación posicional entonces el valor de cada dígito depende de la posición que tiene en el número, así por ejemplo el número 110101_b es:

1*(2⁰) + 0*(2¹) + 1*(2²) + 0*(2³) + 1*(2⁴) + 1*(2⁵) = 1 + 4 + 16 + 32 = 53_d

La computadora está diseñada sobre la base de numeración binaria (base 2). Por eso este caso particular merece mención aparte. Siguiendo las reglas generales para cualquier base expuestas antes, tendremos que:

Existen dos dígitos (0 o 1) en cada posición del número.

Numerando de derecha a izquierda los dígitos de un número, empezando por cero, el valor decimal de la posición es 2n.

Por ejemplo,1101₂ (en base 2) quiere decir:

1*(2³) + 1*(2²) + 0*(2¹) + 1*(2⁰) = 8 + 4 + 0 + 1 = 13₁₀

Sistema Octal

El sistema de numeración octal es también muy usado en la computación por tener una base que es potencia exacta de 2 o de la numeración binaria. Esta característica hace que la conversión a binario o viceversa sea bastante simple. El sistema octal usa 8 dígitos (0,1,2,3,4,5,6,7) y tienen el mismo valor que en el sistema de numeración decimal. Como el sistema de numeración octal usa la notación posicional entonces para el número 3452.32_q tenemos:

2*(8⁰) + 5*(8¹) + 4*(8²) + 3*(8³) + 3*(8^-1) + 2*(8^-2) = 2 + 40 + 4*64 + 64 + 3*512 + 3*0.125 + 2*0.015625 = 2 + 40 + 256 + 1536 + 0.375 + 0.03125 = 1834 + 40625_dentonces, 3452.32_q = 1834.40625_d

El subindice q indica número octal, se usa la letra q para evitar confusión entre la letra o y el número 0. 

Sistema Hexadecimal

Un gran problema con el sistema binario es la verbosidad. Para representar el valor 20210 se requieren ocho dígitos binarios, la versión decimal sólo requiere de tres dígitos y por lo tanto los números se representan en forma mucho más compacta con respecto al sistema numérico binario. Desafortunadamente las computadoras trabajan en sistema binario y aunque es posible hacer la conversión entre decimal y binario, ya vimos que no es precisamente una tarea cómoda. El sistema de numeración hexadecimal, o sea de base 16, resuelve este problema (es común abreviar hexadecimal como hex aunque hex significa base seis y no base dieciseis). El sistema hexadecimal es compacto y nos proporciona un mecanismo sencillo de conversión hacia el formato binario, debido a ésto, la mayoría del equipo de cómputo actual utiliza el sistema numérico hexadecimal. Como la base del sistema hexadecimal es 16, cada dígito a la izquierda del punto hexadecimal representa tantas veces un valor sucesivo potencia de 16, por ejemplo, el número 123416 es igual a:

1*163 + 2*162 + 3*161 + 4*160

lo que da como resultado:

4096 + 512 + 48 + 4 = 466010

Cada dígito hexadecimal puede representar uno de dieciseis valores entre 0 y 1510. Como sólo tenemos diez dígitos decimales, necesitamos inventar seis dígitos adicionales para representar los valores entre 1010 y 1510. En lugar de crear nuevos simbolos para estos dígitos, utilizamos las letras A a la F. La conversión entre hexadecimal y binario es sencilla, considere la siguiente tabla:

Binario             Hexadecimal 
  
  0000                   0 
  0001                   1 
  0010                   2 
  0011                   3 
  0100                   4 
  0101                   5 
  0110                   6 
  0111                   7 
  1000                   8 
  1001                   9 
  1010                   A 
  1011                   B 
  1100                   C 
  1101                   D 
  1110                   E 
  1111                   F

Esta tabla contiene toda la información necesaria para convertir de binario a hexadecimal y visceversa. Para convertir un número hexadecimal en binario, simplemente sustituya los correspondientes cuatro bits para cada dígito hexadecimal, por ejemplo, para convertir 0ABCDh en un valor binario:

0 A B C D (Hexadecimal)
0000 1010 1011 1100 1101 (Binario)

Por comodidad, todos los valores numéricos los empezaremos con un dígito decimal; los valores hexadecimales terminan con la letra h y los valores binarios terminan con la letra b. La conversión de formato binario a hexadecimal es casi igual de fácil, en primer lugar necesitamos asegurar que la cantidad de dígitos en el valor binario es múltiplo de 4, en caso contrario agregaremos ceros a la izquierda del valor, por ejemplo el número binario 1011001010, la primera etapa es agregarle dos ceros a la izquierda para que contenga doce ceros: 001011001010. La siguiente etapa es separar el valor binario en grupos de cuatro bits, así: 0010 1100 1010. Finalmente buscamos en la tabla de arriba los correspondientes valores hexadecimales dando como resultado, 2CA, y siguiendo la convención establecida: 02CA_h. 

El sistema numérico decimal

El sistema de numeración decimal es el más usado, tiene como base el número 10, o sea que posee 10 dígitos (o simbolos) diferentes (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). El sistema de numeración decimal fué desarrollado por los hindúes, posteriormente lo introducen los árabes en Europa, donde recibe el nombre de sistema de numeración decimal o arábigo. Si se aplica la notación posicional al sistema de numeración decimal entonces el dígito número n tiene el valor: (10ⁿ)* A

Este valor es positivo y es mayor o igual que uno si el dígito se localiza a la izquierda del punto decimal y depende del dígito A, en cambio el valor es menor que uno si el dígito se localiza a la derecha del punto decimal. Por ejemplo, el número 3489.125 expresado en la notación posicional

m = posición del dígito que se localiza a la derecha
k = posición del dígito que se localiza a la izquierda
b = valor de la base
n = posición del dígito a evaluar
a = dígito a evaluar

para el ejemplo:

= 5*(10^-3) + 2*(10^-2) + 1*(10^-1) + 9*(10⁰) + 8*(10¹) + 4*(10²) + 3*(10³)
= 0.005 + 0.02 + 0.1 + 9 + 80 + 400 + 3000
= 3489.125

Notación Posicional del Sistema

(10^-6) = 0.000001
(10^-5) = 0.00001
(10^-4) = 0.0001
(10^-3) = 0.001
(10^-2) = 0.01
(10^-1) = 0.1
(10⁰) = 1
(10¹) = 10
(10²) = 100
(10³) = 1000
(10⁴) = 10000
(10⁵) = 100000
(10⁶) = 10000000 
 

compuertas logicas

Compuertas Lógicas

Las compuertas lógicas son dispositivos que operan con aquellos estados lógicos mencionados en la página anterior y funcionan igual que una calculadora, de un lado ingresas los datos, ésta realiza una operación, y finalmente, te muestra el resultado.

Cada una de las compuertas lógicas se las representa mediante un Símbolo, y la operación que realiza (Operación lógica) se corresponde con una tabla, llamada Tabla de Verdad, vamos con la primera...

.: Compuerta NOT

Se trata de un inversor, es decir, invierte el dato de entrada, por ejemplo; si pones su entrada a 1 (nivel alto) obtendrás en su salida un 0 (o nivel bajo), y viceversa. Esta compuerta dispone de una sola entrada. Su operación lógica es s igual a a invertida

.: Compuerta AND

Una compuerta AND tiene dos entradas como mínimo y su operación lógica es un producto entre ambas, no es un producto aritmético, aunque en este caso coincidan.

*Observa que su salida será alta si sus dos entradas están a nivel alto*

.: Compuerta OR

Al igual que la anterior posee dos entradas como mínimo y la operación lógica, será una suma entre ambas... Bueno, todo va bien hasta que 1 + 1 = 1, el tema es que se trata de una compuerta O Inclusiva es como a y/o b

*Es decir, basta que una de ellas sea 1 para que su salida sea también 1*

.: Compuerta OR-EX o XOR

Es OR EXclusiva en este caso con dos entradas (puede tener mas, claro...!) y lo que hará con ellas será una suma lógica entre a por b invertida y a invertida por b.

*Al ser O Exclusiva su salida será 1 si una y sólo una de sus entradas es 1*

Compuertas Lógicas Combinadas.

Al agregar una compuerta NOT a cada una de las compuertas anteriores, los resultados de sus respectivas tablas de verdad se invierten, y dan origen a tres nuevas compuertas llamadas NAND, NOR y NOR-EX... Veamos ahora como son y cual es el símbolo que las representa...

.: Compuerta NAND

Responde a la inversión del producto lógico de sus entradas, en su representación simbólica se reemplaza la compuerta NOT por un círculo a la salida de la compuerta AND.

.: Compuerta NOR

El resultado que se obtiene a la salida de esta compuerta resulta de la inversión de la operación lógica o inclusiva es como un no a y/o b. Igual que antes, solo agregas un círculo a la compuerta OR y ya tienes una NOR.

.: Compuerta NOR-EX

Es simplemente la inversión de la compuerta OR-EX, los resultados se pueden apreciar en la tabla de verdad, que bien podrías compararla con la anterior y notar la diferencia, el símbolo que la representa lo tienes en el siguiente gráfico.

.: Buffer's

Ya la estaba dejando de lado..., no se si viene bien incluirla aquí pero de todos modos es bueno que la conozcas, en realidad no realiza ninguna operación lógica, su finalidad es amplificar un poco la señal (o refrescarla si se puede decir). Como puedes ver en el siguiente gráfico, la señal de salida es la misma que de entrada.
Hasta aquí de teoría, nos interesa más saber como se hacen evidente estos estados en la práctica, y en qué circuitos integrados se las puede encontrar y más adelante veremos unas cuantas leyes que se pueden aplicar a estas compuertas para obtener los resultados que deseas...

Circuitos Integrados y Circuito de Prueba.

Existen varias familias de Circuitos integrados, pero sólo mencionaré dos, los más comunes, que son los TTL y CMOS:

Estos Integrados los puedes caracterizar por el número que corresponde a cada familia según su composición. Por ejemplo;

Los TTL se corresponden con la serie 5400, 7400, 74LSXX, 74HCXX, 74HCTXX etc. algunos 3000 y 9000.

Los C-MOS y MOS se corresponde con la serie CD4000, CD4500, MC14000, 54C00 ó 74C00. en fin...

La pregunta de rigor... Cual es la diferencia entre uno y otro...?, veamos... yo comencé con los C-MOS, ya que disponía del manual de estos integrados, lo bueno es que el máximo nivel de tensión soportado llega en algunos casos a +15V, (especial para torpes...!!!), mientras que para los TTL el nivel superior de tensión alcanza en algunos casos a los +12V aproximadamente, pero claro estos son límites extremos, lo común en estos últimos es utilizar +5V y así son felices.

Otra característica es la velocidad de transmisión de datos, resulta ser, que los circuitos TTL son mas rápidos que los C-MOS, por eso su mayor uso en sistemas de computación.

Suficiente... de todos modos es importante que busques la hoja de datos o datasheet del integrado en cuestión, distribuido de forma gratuita por cada fabricante y disponible en Internet... donde más...?

Veamos lo que encontramos en uno de ellos; en este caso un Circuito integrado 74LS08, un TTL, es una cuádruple compuerta AND. Es importante que notes el sentido en que están numerados los pines y esto es general, para todo tipo de integrado...

Comenzaremos con este integrado para verificar el comportamiento de las compuertas vistas anteriormente. El representado en el gráfico marca una de las compuertas que será puesta a prueba, para ello utilizaremos un fuente regulada de +5V, un LED una resistencia de 220 ohm, y por supuesto el IC que corresponda y la placa de prueba.

El esquema es el siguiente...
En el esquema está marcada la compuerta, como 1 de 4 disponibles en el Integrado 74LS08, los extremos a y b son las entradas que deberás llevar a un 1 lógico (+5V) ó 0 lógico (GND), el resultado en la salida s de la compuerta se verá reflejado en el LED, LED encendido (1 lógico) y LED apagado (0 lógico), no olvides conectar los terminales de alimentación que en este caso son el pin 7 a GND y el 14 a +5V. Montado en la placa de prueba te quedaría algo así...
Esto es a modo de ejemplo, Sólo debes reemplazar IC1, que es el Circuito Integrado que está a prueba para verificar su tabla de verdad.

Un poco de Leyes.

Antes de seguir... Lo primero y más importante es que trates de interpretar la forma en que realizan sus operaciones cada compuerta lógica, ya que a partir de ahora las lecciones se complican un poco más. Practica y verifica cada una de las tablas de verdad.

.: Leyes de De Morgan

Se trata simplemente de una combinación de compuertas, de tal modo de encontrar una equivalencia entre ellas, esto viene a consecuencia de que en algunos casos no dispones del integrado que necesitas, pero si de otros que podrían producir los mismos resultados que estas buscando.

Para interpretar mejor lo que viene, considera a las señales de entrada como variables y al resultado como una función entre ellas. El símbolo de negación (operador NOT) lo representaré por "~", por ejemplo: a . ~ b significa a AND NOTb, se entendió...?

.: 1º Ley:

El producto lógico negado de varias variables lógicas es igual a la suma lógica de cada una de dichas variables negadas. Si tomamos un ejemplo para 3 variables tendríamos..
~ (a.b.c) = ~a + ~b + ~c El primer miembro de esta ecuación equivale a una compuerta NAND de 3 entradas, representada en el siguiente gráfico y con su respectiva tabla de verdad.
El segundo miembro de la ecuación se lo puede obtener de dos formas...
Fíjate que la tabla de verdad es la misma, ya que los resultados obtenidos son iguales. Acabamos de verificar la primera ley.

.: 2º Ley:

La suma lógica negada de varias variables lógicas es igual al producto de cada una de dichas variables negadas...
~ (a + b + c) = ~a . ~b . ~c El primer miembro de esta ecuación equivale a una compuerta NOR de 3 entradas y la representamos con su tabla de verdad...
El segundo miembro de la ecuación se lo puede obtener de diferentes forma, aquí cité solo dos...
Nuevamente... Observa que la tabla de verdad es la misma que para el primer miembro en el gráfico anterior. Acabamos así de verificar la segunda ley de De Morgan.

Para concluir... Con estas dos leyes puedes llegar a una gran variedad de conclusiones, por ejemplo...

Para obtener una compuerta AND puedes utilizar una compuerta NOR con sus entradas negadas, o sea...
a . b = ~( ~a + ~b) Para obtener una compuerta OR puedes utilizar una compuerta NAND con sus entradas negadas, es decir...
a + b =~( ~a . ~b) Para obtener una compuerta NAND utiliza una compuerta OR con sus dos entradas negadas, como indica la primera ley de De Morgan...
~ (a.b) = ~a + ~b Para obtener una compuerta NOR utiliza una compuerta AND con sus entradas negadas, ...eso dice la 2º ley de De Morgan, así que... habrá que obedecer...
~(a + b) = ~a . ~b La compuerta OR-EX tiene la particularidad de entregar un nivel alto cuando una y sólo una de sus entradas se encuentra en nivel alto. Si bien su función se puede representar como sigue...
s = a . ~b + ~a . b te puedes dar cuenta que esta ecuación te indica las compuertas a utilizar, y terminarás en esto...
Para obtener una compuerta NOR-EX agregas una compuerta NOT a la salida de la compuerta OR-EX vista anteriormente y ya la tendrás. Recuerda que su función es...
s = ~(a . ~b + ~a . b) Para obtener Inversores (NOT) puedes hacer uso de compuertas NOR o compuertas NAND, simplemente uniendo sus entradas.